Le paradoxe de l’Indice de Masse Corporelle ou IMC

Merci à Olivier pour avoir planté l’idée d’un tel article

A l’heure des bonnes résolutions de nouvelle année, une résolution récurrente est celle de la perte de poids. Mais combien de kg faut-il perdre ? Vers quel poids faut-il tendre? Pas forcément évident de le savoir et une formule mathématique semble en avoir la réponse. Cette formule est l’Indice de Masse Corporelle ou IMC ou encore l’Index de Quetelet.

Cette formule d’IMC fait la Une depuis quelques années. Pourtant elle ne date pas d’hier, en effet Adolphe Quetelet l’avait développé entre 1830 et 1850 !

Pourquoi cette formule est en fait doublement paradoxale…

Alors qu’est-ce que cette formule d’IMC ?

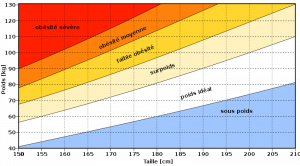
L’IMC est un indicateur qui permet de définir si un individu est en sous-poids ,sur-poids, ou possède un poids « normal » pour sa taille.

La formule est la suivante:

IMC= (Masse en kg)/ (taille en m)^2

Voici les interprétations des résultats:

• moins de 16,5: dénutrition
• Entre 16,5 et 18,5: maigreur
• entre 18,5 et 24,9: corpulence normale
• entre 25 et 30: surpoids
• entre 30 à 35: obésité modérée
• entre 35 à 40: obésité sévère
• plus de 40: obésité morbide ou massive

Cet Indice de Masse Corporelle permet donc d’avoir une idée de la santé pondéral d’une personne. Si cet indice est trop faible ou trop élevé alors la santé de l’individu est à risque.

Cet IMC a ses limites, les personnes trop grandes ou trop petites, les femmes enceintes, les enfants, les sportifs intensifs et les personnes âgées se voient être exclus de l’application de cette formule.

Le paradoxe de l’Indice de Masse Corporelle ou IMC

Nous n’allons pas parler du paradoxe du sportif et de son IMC élevé alors qu’il n’aura que peu de tissus adipeux. Les muscles étant plus lourds que la graisse son IMC grimpe en flêche alors qu’il est en excellente santé. Ce « paradoxe » est d’une banalité extrême et est parfaitement représenté par la caricature en début de page. Mais intéressons nous à une autre sorte de paradoxe.

Pourquoi l’IMC serait-il illogique ?

L’évolution du poids d’un individu ne se fait pas au carré de sa taille mais au cube de sa taille.

explication:

Imaginons un homme de 1m80 et de 80kg. Son IMC sera de 24,69.

Imaginons que cet homme toutes proportions gardées soit 2 fois plus grand. Soit 3m60, quel devrait alors être son poids ?

• Non son poids ne devrait être pas le double.
• Si nous utilisons le principe qu’il aura le même IMC alors on obtient le calcul suivant: poids=3,6^2 x 24,69=320kg. Cet homme devrait alors peser 320kg pour 3m60 de haut. Mais ce résultat est aussi erroné.

Réponse: Si cet homme est 2 fois plus grand mais conserve les mêmes proportions alors son poids véritable sera 640kg ! pourquoi? parce que la masse dépend du volume et si cette personne est 2 fois plus grande alors cette personne est aussi 2 fois plus large, ainsi que 2 fois plus profonde: ce qui équivaut à être 8 fois plus volumineuse!!! Donc 8 fois plus lourde. Son IMC fait donc un magistral 49,3 et la place dans le rang des morbidement et excessivement obèses alors qu’elle est tout à fait bien proportionnée pour sa taille !

C’est pourquoi il existe un illogisme dans cet IMC car il tient compte d’une surface par rapport à la taille alors que le poids fluctue en fonction d’un volume!

Le graphe et le tableau suivant compare l’évolution de l’IMC avec l’évolution de l’« indice de masse volumique corporelle » (l’IMVC garde une proportion de la masse en fonction du volume):

• Il y a 2 courbes rose-rouge d’IMC: une qui détermine le poids en fonction de la taille pour un IMC de 20,76 et l’autre pour un IMC de 24,22. Ces 2 nombres sont dans la limite « saine » de l’IMC.
• Les 2 courbes vertes représentent l’indice de masse volumique corporelle. C’est à dire que c’est le poids que devrait vraiment faire un individu en fonction de sa taille si il était bien proportionné. Les proportions sont basées sur une personne de 1m70 et qui pèse 60kg (IMC 20,76) et aussi 70kg (IMC 24,22)

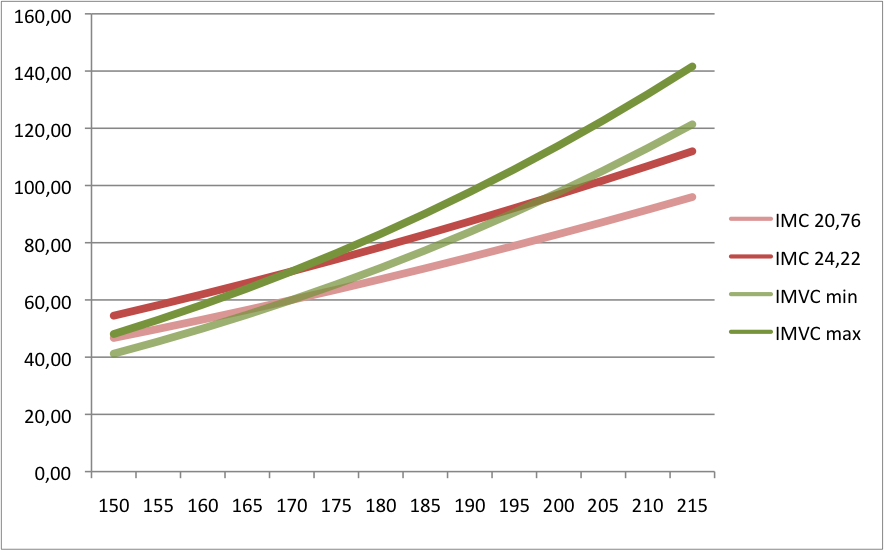
Comparaison du poids en fonction de la taille en suivant l’IMC et l’IMVC

Sur ce graphe nous pouvons voir clairement que l’indice de masse volumique corporelle est beaucoup plus permissive au niveau du poids que l’IMC dès lors que la taille augmente de manière significative.

Pourquoi alors ne pas tenir compte d’un IMC basé sur le volume ?

Paradoxalement ceci serait en fait illogique !

Ne vous inquiétez pas vous allez comprendre.

Notre poids est fonction du volume qui augmente au cube par rapport à notre taille, alors que nos surfaces articulaires, elles, augmentent au carré par rapport à notre taille. C’est l’explication d’un des résultats précédents. L’IMC de 49,3 de notre géant de 3m60 qui est bien proportionné. Les pressions sur les articulations porteuses et les os vont être 2 fois plus fortes alors que les proportions sont bien gardées!

Imaginez le problème d’un volume musculaire qui augmente au cube et qui tire sur un tendon dont la section augmente au carré!?

Et imaginez aussi un volume sanguin augmentant lui aussi au cube alors que la section de la tuyauterie, elle, augmente au carré !

Notre pauvre géant bien proportionné souffrira à coup sûr de tassements de vertèbres, de hernies discales, de déchirures musculaires et d’hypertension artérielle !

Conclusion:

Ainsi l’IMC permet de garantir une certaine cohérence de volume sanguin par rapport au diamètre de sections des artères et veines du corps, ainsi qu’une cohérence articulaire et musculaire.

Il est du coup intéressant de voir que si une personne de très grande taille veut conserver un IMC « normal » afin de protéger son coeur et ses articulations alors elle devient rapidement longiligne.